this is what happens when you try to convert mathematical structures into music
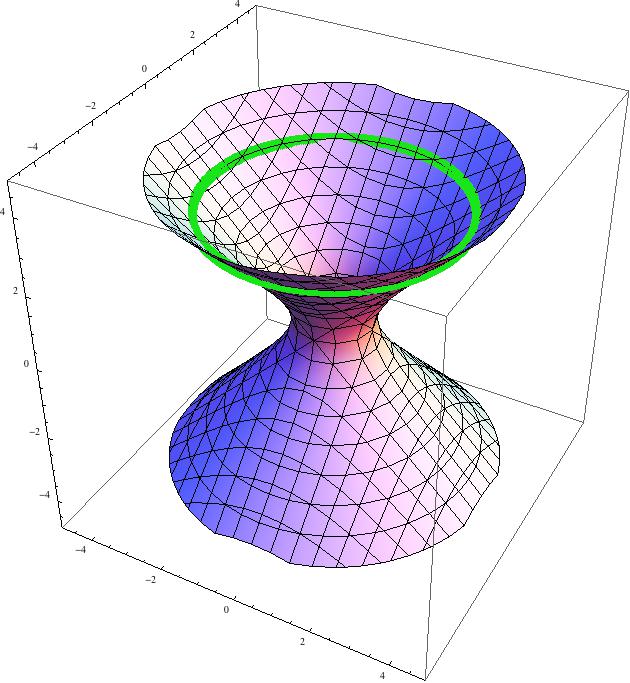
I'll start with what I will call "hyperbolic music" because it resulted from tinkering with integer points on the rotational hyperboloid - a geometrical structure that you see in the next plot. Mathematically speaking it is just a set of points in 3D space satisfying the equation: x^2+y^2-z^2=1

Integer points are just points on that surface that happen to have integer coordinates - and there are plenty of them, for instance (4,7,8), (8,9,12), (14,17,22), (26,15,30) and so on.
Since there are infinitely many such points, I will keep track of them by focusing on the circles with constant z (you can see one in the picture in green). I will call such circles "levels" and from now on will consider only levels with an even value of z.
I am going to project all "even" levels down onto the x-y plane by "forgetting" about the z coordinate. All integer points on even levels have even value of z (by definition) and different parity for the remaining coordinates. When x is even, I plot the point in blue, otherwise I plot it in red. The sketch of integer points on even levels from 2 to 60 is on the next plot.

You can see that each level has a trivial point with coordinates (z,1,z) or (1,z,z) - that is the horizontal blue or vertical red row respectively. I will disregard these points and concentrate on the non trivial solutions with even value of x (the remaining blue points). Here is a list of the first such points (on even levels):
(4,7,8)
(8,9,12)
(6,17,18)
(10,15,18)
(14,17,22)
(16,23,28)
(26,15,30)
etc.
Each point will be assigned pitch and duration (length) as follows: I will project the point (yellow line) onto the green-purple screen at the boundary and assign a pitch to every segment from a given table of tones (whether harmonic or atonal). If the given level contains two or more points (and in higher levels it occurs quite frequently) I will play them in harmony. The number of such tones at each level z is essentially determined by the number of factors of a complex number z+i. The length of each tone will correspond to the distance from the previous "non-trivial" level. Since the smallest distance between the levels is 2 - that will corresponds to the shortest length, let's call it L. Everything else will be an integer multiple of this length. For instance the point (6,17,18) on the plot (which the yellow line goes through) intersects the screen at the fourth "bracket" from the left (that determines its pitch) and since the previous non trivial level is 12, I will assign the duration 3L to it.
And now some examples of this process for different MIDI instruments. They are played with different tempo and they all start at different levels of the hyperboloid (going up from there). The "Atonal" means I assign the colored sectors on the boundary to the chromatic scale. In the remaining cases, the scale is stated explicitly.
Atonal Hyperbolic Etude (xylophone, start at 1100)
Hyperbolic Etude in E major (xylophone, start at 300)
Hyperbolic Etude in C major (synthetic voice, start at 1700)
Hyperbolic Fugue in E major (choir, piano and marimba, start at 3910)
Hyperbolic Fugue in C major (organ, oboe and viola, start at 930)
The etudes are derived from the hyperboloid as described above. The fugues come from a combination of three hyperboloids of the form x^2+y^2-z^2 = k^2 for suitably chosen k. Note that they have different non trivial levels so the three voices start at different points in time and that's what gives the music an air of a fugue)
(additional pieces - somewhat longer)
Atonal Hyperbolic Scherzo (4:25)
Hyperbolic Scherzo in E major (3:56)
Prime Number Ballad (5:50)
Duelling Sinusoids (5:31)
The rest of this page will be a temporary home for some music that I wrote in the past. It was created with the electronic help of my first keyboard - Yamaha PSR-500, which was really a toy for kids, but it served its purpose of getting me hooked on piano, so I am not going to say anything bad about it. Most of these pieces were recorded by plugging the headphones outlet of the keyboard directly into a CD recorder, so do not expect too much in terms of sound quality. I am primarily using this webpage as a repository of musical ideas (especially the second series has this character). If I ever learn how to play piano properly, I will remake them on a reasonably decent instrument.
A friendly warning: the files below (*.mp3) are fairly large - about 1.5M/min.
|
1. Happy Birthday, Little Witch (5:03) 2. That Which Never Knocks (4:09) 3. Cha-Cha (3:44) 4. Why Mice Have Ears (3:02) 5. Flying Grapes (2:45) 6. Messenger for the Queen (3:41) 7. Sail for Sale (4:22) 8. Dancing Queen (5:52) 9. Undanced Waltz (8:12) 10. Silky Way (2:53) 11. Mermaid in the Pool (4:42) 12. Bar Closes at 4am (2:27) 13. Poker Players (2:39) 14. Not At All (4:21) 15. 94 Fahrenheit (3:53) 16. Promised Land (5:14) 17. La Fionco (2:33) 18. Prelude (2:08) 19. Miss 2508 (4:28) Nest of Wolves got mildly damaged during copying, plus it was an odd piece anyway, but for the sake of completeness:
|
© 1993 Jan Rehacek
© 2004 Jan Rehacek
feedback: trumpeta8 at yahoo dot com